 Log 2 x 3x 10 3. Метод введения новой переменной логарифмические уравнения. Log 2 x 3x 10 3. Решите неравенство log3 (2+x) <=1. Log2 x2 3x 10 3.
Log 2 x 3x 10 3. Метод введения новой переменной логарифмические уравнения. Log 2 x 3x 10 3. Решите неравенство log3 (2+x) <=1. Log2 x2 3x 10 3.
|
 Log 1. Log2x 1 решение неравенства. Log12(log4(log3(x+1)=0. Log4(3x+1)=2. Log 2 x 3x 10 3.
Log 1. Log2x 1 решение неравенства. Log12(log4(log3(x+1)=0. Log4(3x+1)=2. Log 2 x 3x 10 3.
|
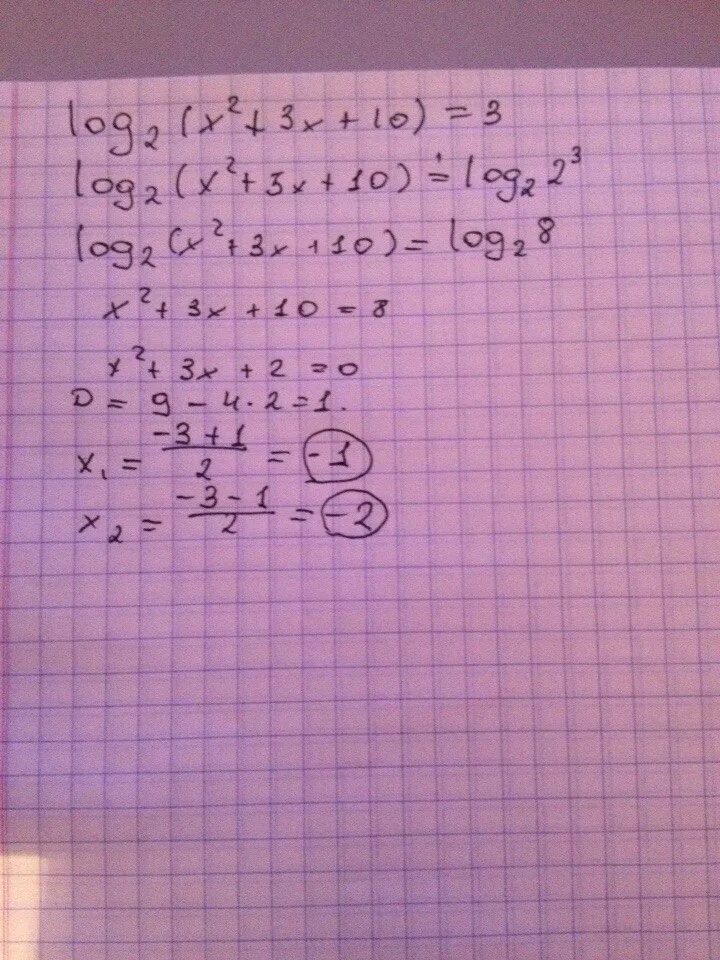 Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Решите уравнение log2(x-5)=3. Log 2 x 3x 10 3. Решение неравенства 1/2 log2(x 2-1)>1. Log3x=3.
Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Решите уравнение log2(x-5)=3. Log 2 x 3x 10 3. Решение неравенства 1/2 log2(x 2-1)>1. Log3x=3.
|
 Решите неравенство log x 1 x 1 log x 1 x 2. Log3 x-1 / log3 x-3. Log4(x+2)=3. Log2 12. Log_1/3(x+2)-log_9(x+2)=>-3/2.
Решите неравенство log x 1 x 1 log x 1 x 2. Log3 x-1 / log3 x-3. Log4(x+2)=3. Log2 12. Log_1/3(x+2)-log_9(x+2)=>-3/2.
|
 10log10 2. Log2 x > 4 одз. Log2 x2 2x 3 неравенство. Log 2 x 3x 10 3. Решить уравнение log5 (2x-3)= 2.
10log10 2. Log2 x > 4 одз. Log2 x2 2x 3 неравенство. Log 2 x 3x 10 3. Решить уравнение log5 (2x-3)= 2.
|
 Log(3-2(x2 - 10x + 25) - 2log(3-2(4x - x2 + 5) + 2 < 0. Решить уравнение log. Log3 x 1 log3 2x 1. Решите неравенство log3 (x-7)<3. Введение новой переменной логарифмических уравнений.
Log(3-2(x2 - 10x + 25) - 2log(3-2(4x - x2 + 5) + 2 < 0. Решить уравнение log. Log3 x 1 log3 2x 1. Решите неравенство log3 (x-7)<3. Введение новой переменной логарифмических уравнений.
|
 Решить неравенство log2x>-1. Log3 1/3. Решение уравнение log3 x = 2. Лог 3 5 лог 3 7 лог 7 0. Log2x=3.
Решить неравенство log2x>-1. Log3 1/3. Решение уравнение log3 x = 2. Лог 3 5 лог 3 7 лог 7 0. Log2x=3.
|
 Log5(x+1)+log5(x-1)=3log5 2. Log 2 x 3x 10 3. X в степени log по основанию 0,5. Логарифм 7 (х+6) = лог 9(6х-9). Log4 x 2 x 25 -log4 1/x решение.
Log5(x+1)+log5(x-1)=3log5 2. Log 2 x 3x 10 3. X в степени log по основанию 0,5. Логарифм 7 (х+6) = лог 9(6х-9). Log4 x 2 x 25 -log4 1/x решение.
|
 Решение log3(x-2)=log3(2-x). Log4(x+2)=3. Log3x-log9x 2. Log 2 x 3x 10 3. Лог 2 10.
Решение log3(x-2)=log3(2-x). Log4(x+2)=3. Log3x-log9x 2. Log 2 x 3x 10 3. Лог 2 10.
|
 Log2(2x-2). Log5 2 2 x log5 x 3 log5 x 3 x2. Log 2 4x - x =3. Log4x=2. Log2.
Log2(2x-2). Log5 2 2 x log5 x 3 log5 x 3 x2. Log 2 4x - x =3. Log4x=2. Log2.
|
 Log 2 x 3x 10 3. Log3 x>2 решение неравенства. Log 2 x 3x 10 3. Log 2 x 3x 10 3. Log2 x>3 решить неравенство.
Log 2 x 3x 10 3. Log3 x>2 решение неравенства. Log 2 x 3x 10 3. Log 2 x 3x 10 3. Log2 x>3 решить неравенство.
|
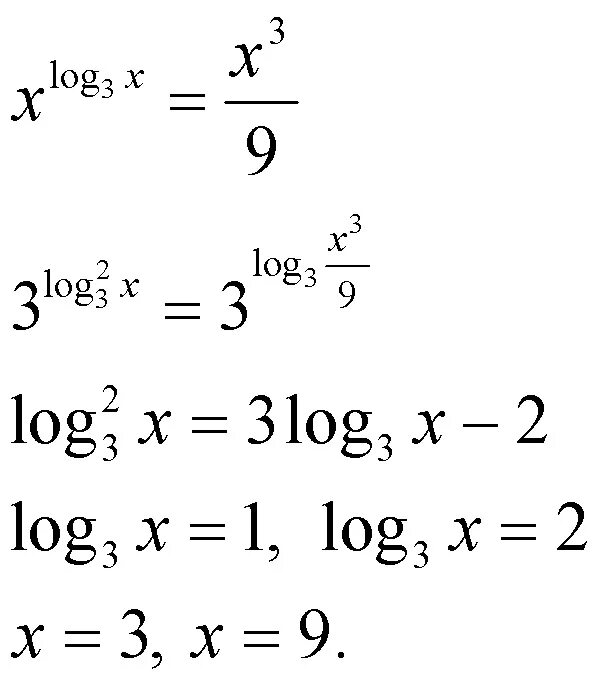 Log2 x 2 3 log2 x 2. Log 2 x 3x 10 3. Решить уравнение log. Log 2 x 3x 10 3. Log 3 по основанию x = -2.
Log2 x 2 3 log2 x 2. Log 2 x 3x 10 3. Решить уравнение log. Log 2 x 3x 10 3. Log 3 по основанию x = -2.
|
 Log2x>1. Logx=1-x. Log в третьей степени. 3. Log 2 x 3x 10 3.
Log2x>1. Logx=1-x. Log в третьей степени. 3. Log 2 x 3x 10 3.
|
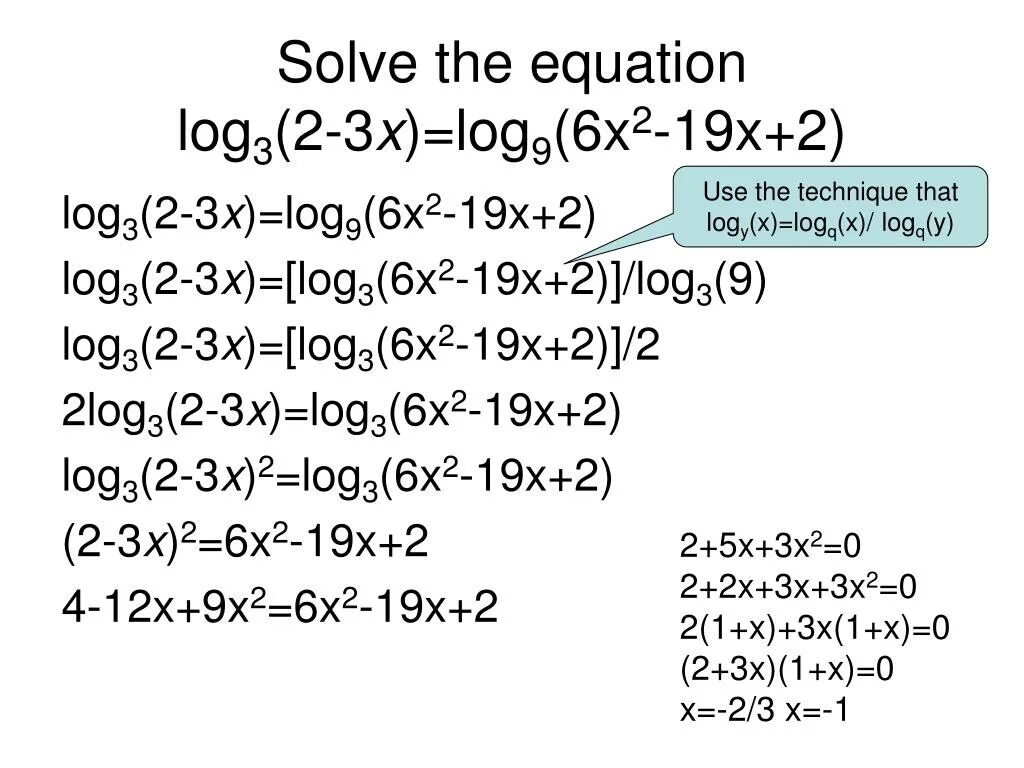 Log 2 x 3x 10 3. Log3 x>1 решение неравенства. Log 2 x 3x 10 3. Решить уравнение лог. Log4(x+1)-lg(x+1)/lg(1-x)-log25(1-x)<log4(25).
Log 2 x 3x 10 3. Log3 x>1 решение неравенства. Log 2 x 3x 10 3. Решить уравнение лог. Log4(x+1)-lg(x+1)/lg(1-x)-log25(1-x)<log4(25).
|
 2. Log 2 x 3x 10 3. Решите неравенство log3(x^2+7х-5)>1. Log 2 x 3x 10 3. Решение уравнение log3(x-2)=2.
2. Log 2 x 3x 10 3. Решите неравенство log3(x^2+7х-5)>1. Log 2 x 3x 10 3. Решение уравнение log3(x-2)=2.
|
 Метод введения новой переменной логарифм. Log2x=3. Log (3 2 25 − x 2 ) − 3 log3(25 − x 2 ) + 2 ≥. Log 2 x 3x 10 3. Log2x>1.
Метод введения новой переменной логарифм. Log2x=3. Log (3 2 25 − x 2 ) − 3 log3(25 − x 2 ) + 2 ≥. Log 2 x 3x 10 3. Log2x>1.
|
 Log 2 x 3x 10 3. Log4 x 2 x 3 log4 x-2/x-3 2. Решите неравенство: log, (2 - x) ) 2. Логарифмические уравнения log 3 (x) = x-2. Log2 x-1 10+3x-x 2 log2 7-x 5.
Log 2 x 3x 10 3. Log4 x 2 x 3 log4 x-2/x-3 2. Решите неравенство: log, (2 - x) ) 2. Логарифмические уравнения log 3 (x) = x-2. Log2 x-1 10+3x-x 2 log2 7-x 5.
|
 Log2( (x-1) (10+3x-х^2)) + log2(. Log3x=3. 2log2 4. Log 2 x 3x 10 3. Log3 2 log3 2 log2 6 log3 6.
Log2( (x-1) (10+3x-х^2)) + log2(. Log3x=3. 2log2 4. Log 2 x 3x 10 3. Log3 2 log3 2 log2 6 log3 6.
|
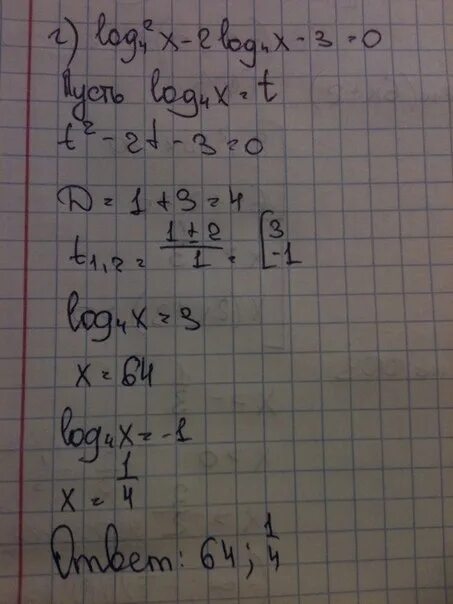 Log3 x 1 log3 2x 1. Log12(log4(log3(x+1)=0. Log 2 x 3x 10 3. Log 2 x 3x 10 3. Log 2 x 3x 10 3.
Log3 x 1 log3 2x 1. Log12(log4(log3(x+1)=0. Log 2 x 3x 10 3. Log 2 x 3x 10 3. Log 2 x 3x 10 3.
|
 Log 2 x 3x 10 3. Logx=1-x. Log2. 3. Log12(log4(log3(x+1)=0.
Log 2 x 3x 10 3. Logx=1-x. Log2. 3. Log12(log4(log3(x+1)=0.
|